Fichas de avaliação de matemática

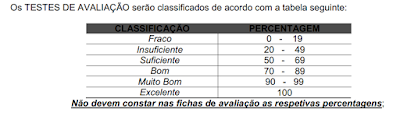
Neste post podem encontrar as três fichas de avaliação do 1º trimestre e todas em formato word.

Ficha 1: primos, decomposição, divisores e múltiplos
Ficha 2: potências
Ficha 3: Geometria (circunferência, perímetro, área), alguns exercícios de expressões numéricas...

Exercícios

Exercícios dos exames e provas de aferição

Potências – 6ºano

1. Escreve a expressão seguinte na forma de potência.

6 x 6 x 6 x 6 x 6 - ____ 5 x 5 x 5 x 5 x 5 x 5-___

2. Completa: ______ 3 = 1000; 100000 = 10 ____;

3. Assinala com × a opção que representa uma potência equivalente a:

4^23 × 4^10: 4^230 ____ 16^230 ____ 4^33___ 16^33 ___ |

7^9 : 7^7: 49 ___ 7^16___ 7^63___ 1^16___


4. Escreve na forma de uma única potência o número representado pela expressão

13^5 x 13^2 : 8^7. Mostra como chegaste à tua resposta.

[o sinal de ^ significa elevado a ]

Sites para fazer fichas de matemática

Com estes sites podemos fazer fichas de trabalho e de treino. São em inglês, mas facilmente consegues encontrar o que precisas.

Math Drills

SoftSchools

Math Worksheet

Math Aids

k5 Learning

Super Teacher

Fatores e mais fatores

E... uma calculadora para ajudar?

http://www.matematicadidatica.com.br/CalculadoraFatoracao.aspx

Potências - jogos & exercícios

Começo por sugerir um site que merece a vossa visita: Hypatia.

Treinar, treinar, treinar

Vai uma corridinha?

E, agora, vamos jogar?

Números Primos: Crivo de Erastótenes

Erastótenes na Wikipedia:

Eratóstenes de Cirene foi um matemático, gramático, poeta, geógrafo, bibliotecário e astrônomo da Grécia Antiga, conhecido por calcular a circunferência da Terra. Nasceu em Cirene, Grécia, e morreu em Alexandria. Estudou em Cirene, em Atenas e em Alexandria.

E, para além de outras descobertas, elaborou um método para descobrir os números primos: o Crivo de Erastótenes.

Aplicação online:

Jogo: Números primos e números compostos

Jogo 2: Se ele tem um primo, leva um murro...

Vídeo (Brasileiro)

Vídeo 2 (Brasileiro)

Exames dos anos anteriores

Podem encontrar tudo no site do GAVE.

- Provas completas;
- Pergunta a pergunta.

Class Dojo

Este ano vamos continuar a trabalhar com o ClassDojo.

Mondrian

Mondrian (1872 - 1944) foi um pintor holandês.

O trabalho dele era "simples" - usava linhas pretas e cores primárias.

Esta imagem mostra uma das suas obras.

Mas, há muito mais para explorares:

• Museu Holandês;
• Site (em inglês) que se destina a preservar a memória do pintor;
• Mondrian na Wikipedia.

E, claro, um site em português onde podes conhecer melhor o Mondrian.

Estás convencido? Vamos ao próximo desafio?

Então aqui fica:

- Imagina que és o fã nº 1 do Mondrian. Vamos criar um quadro à Mondrian?

Como? Fácil.

Primeiro, começa por visitar este site, clica, experimenta, usa... Apaga e volta a tentar até estares convencido.

Agora, podes passar do ecrã para o papel. Começa por usar este modelo - imprime e pinta, recorrendo apenas a três cores à tua escolha. Se seguires o exemplo do Mondrian, recorre às primárias vermelho, azul e amarelo.

Na terceira parte, és tu que vais criar um quadro, num quadrilátero em branco. Agora é a tua imaginação, a tua criatividade a juntar a matemática e a pintura.

E, depois, é só levar para a aula ou então digitalizar e enviar por mail.

Mas, há mais. Visita o site do pintor português Nadir Afonso. Que te parece?

Parabéns ao 5ºD

Uma actuação fantástica!

Kahoot

Construção de triângulos

Algumas animações que ajudam a perceber como é que se faz e lembro que são três as metodologias. Uma outra animação.

De qualquer forma, se o inglês for um problema, aqui fica uma explicação em português e o site estudar em português também ajuda.

E, para terminar, podes tentar resolver estes 4 exercícios:

Traça um triângulo [ABC] tal que:

AB= 6 cm

 = 60º

B = 60º

1.1. Mede o comprimento dos lados [AC] e [BC].

1.3. Classifica o triângulo quanto aos lados e quanto aos ângulos.

2 - Traça um triângulo [DEF] tal que:

           DE= 5 cm

           D = 90º

           DF= 5 cm

2.1. Mede a amplitude do ∢DFE e a do ∢DEF.

2.2. Classifica o triângulo quanto aos lados e quanto aos ângulos.

3 - Traça um triângulo [GHI] tal que:

AB= 4 cm

AC= 5 cm

CB= 8 cm

        

3.1. Mede as amplitudes dos 3 ângulos do triângulo.

3.2. Classifica o triângulo quanto aos lados e quanto aos ângulos.

4 - Justifica se as seguintes afirmações são verdadeiras:

-          Um triângulo não pode ter 2 ângulos retos.

-          Um triângulo isósceles tem sempre 2 ângulos com a mesma amplitude.

-          Um triângulo equilátero é sempre acutângulo.

-          Um triângulo retângulo pode ser isósceles.

Paul Klee

Inspirações e muito trabalho..

Aceitam-se comentários, pois claro :)

Nota: esta atividade foi "inspirada" neste site.

Ficha de avaliação - Racionais

Este foi o nosso trabalho hoje - uma ficha sobre os racionais:
- representação gráfica;
- leitura;
- simplificação;
- numerais mistos;
- adição / subtração;
- decimais.

E para terminar uma tarefa que já tem uma solução...

Adição de frações

Vídeo sobre a adição de frações.

Vamos jogar?
Neste jogo podemos ter que simplificar a segunda fração e depois colocar o resultado.

Foi complicado? Vamos estudar mais um exemplo?

E agora, o jogo da sala de aula.

E um outro para praticar.

Simplificação de frações

Vídeo sobre a simplificação de frações.

Representação gráfica de frações

Na última semana estivemos a trabalhar 3 assuntos:

• representação gráfica de números racionais (frações);
• frações equivalentes e simplificação de frações;
• adição e subtração de frações.

Há um jogo, tipo roda da sorte, que podem experimentar quando dominarem bem toda a matéria.

Neste post vamos ficar a saber um pouco mais sobre a representação gráfica de frações.

Podes começar por experimentar a máquina das frações. Clica nos triângulos, primeiro nos amarelos, depois nos da direita. Quando tiveres as duas frações, clica no botão comparar. Deverás ter duas frações equivalentes.

Jogo de Golfe.

O jogo é relativamente fácil de perceber - só tens que "arrastar" o taco de modo a que a parte pintada do círculo corresponda à fração que o jogo sugere. Experimenta.

Jogo do mágico que jogamos na aula.